A quick proof that the puzze game Inertia (see this version on Simon Tatham’s Portable Puzzle Collection) is NP-complete.

The rules of the game are:

• You are a small green ball sitting in a grid full of obstacles. Your aim is to collect all the gems without running into any mines.
• You can move the ball in any orthogonal or diagonal direction. Once the ball starts moving, it will continue until something stops it. A wall directly in its path will stop it (but if it is moving diagonally, it will move through a diagonal gap between two other walls without stopping). Also, some of the squares are ‘stops’; when the ball moves on to a stop, it will stop moving no matter what direction it was going in. Gems do not stop the ball; it picks them up and keeps on going.
• Running into a mine is fatal. Even if you picked up the last gem in the same move which then hit a mine, the game will count you as dead rather than victorious.

We can transform the game into a decision problem: “Given an $n \times n$ Inertia level, is it solvable?”

Theorem: The decision problem INERTIA is NP-complete.

The problem is in NP: if the level is solvable then a polynomial time solution exists; indeed, suppose that there are $m$ gems in the solution, and $g_1,g_2,..,g_m$ is the order in which they are picked. Then from $g_i$ to $g_{i+1}$ the green ball can traverse a maximum of $n^2$ cells because there is no need to visit the same cell twice (the other elements of the game are fixed). The same argument can be applied to the path from the starting position and gem $g_1$. Furthermore, given a solution it can be easily checked in polynomial time.

To show that the problem is NP-hard we use a polynomial time reduction from the following NPC problem [1]: the Hamiltonian circuit problem in planar digraphs such that for all vertices $v$:

$\mbox{indegree}(v)+\mbox{outdegree}(v)=3$

We can simulate the traversal of a planar digraph $G$ using the following two gadgets to represent its nodes:

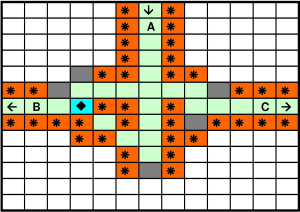Gadget 1: the green ball can enter the gadget only from $A$, after picking the gem it can leave the gadget from $B$ or $C$ (represents a indegree=1, outdegree=2 node).

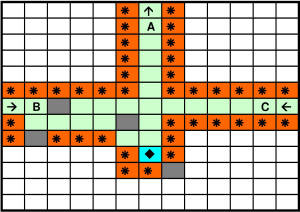Gadget 2: the green ball can enter the gadget only from $B$ or $C$; after picking the gem it can leave the gadget only from $A$ (represents an indegree 2, outdegree 1 node).

The gadgets are $15 \times 15$ grids and can be rotated. Furthermore, in order  to replicate the planar digraph $G$, we can easily build straight links or curves among the gadgets using corridors made with solid blocks (and if nedeed we can also build gadgets to simulate nodes with indegree=3 or nodes with outdegree=3).

The construction of the Inertia level can be done in polynomial time: build an orthogonal representation of $G$ [2] and scale it ($\times 15$) in order to make enough space to replace the nodes with a corresponding gadget. Replace the orthogonal lines with the corridors and put the green ball (the starting node) on the exit of a gadget that represent a node with outdegree=1 (it can be easily proved that if such node doesn’t exist then $G$ doesn’t have an Hamiltonian cycle).

The original planar digraph $G$ has an Hamiltonian cycle if and only if the corresponding Inertia level has a solution. By construnction an Hamiltonian cycle is also a valid solution to the Inertia level. The other way, if $G$ has a solution, then the green ball must exit from the starting node without picking its gem, must traverse all gadgets using exactly one entrance and one exit and finally it must return to the starting gadget to pick its gem. The path followed by the ball corresponds to a cycle in $G$ that visits all nodes and uses exactly two edges for every nodes; so it is an Hamiltonian path.

$\square$

[1] Michael R. Garey and David S. Johnson. 1979. Computers and Intractability: A Guide to the Theory of Np-Completeness. W. H. Freeman & Co., New York, NY, USA.

[2] Giuseppe Di Battista, Peter Eades, Roberto Tamassia, and Ioannis G. Tollis. 1994. Algorithms for drawing graphs: an annotated bibliography. Comput. Geom. Theory Appl. 4, 5 (October 1994), 235-282.