While thinking about simple “puzzles” that seem hard at a first glance, but have not enough rules and structural constraints that make it easy to prove that they are NP-complete, I designed the following game (but perhaps it has already a name … let me know if you know it 🙂 ):
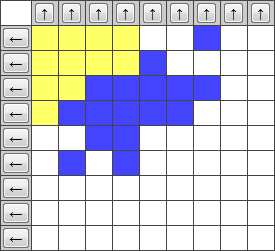
- a $N \times N$ grid contains $S \times S$ blue boxes in the upper left area, the home area; each box occupies a cell;
- a column (or row) that contains at least one box is picked at random and it is shifted downward (or rightward). If a box exits from one border it re-enters on the opposite site;
- the random shift is repeated maxmoves times (e.g. $maxmoves = S^2$);
- the aim of the game is to repack the boxes in the upper left home area, using at most maxmoves upward column shifts or leftward row shifts.
A simple javascript version of the game can be played here.
The rules are simple, but even in a small game with a 4×4 home area it’s hard to find the correct shift sequence …
The Box Shift Puzzle could be analyzed from a computational complexity perspective:
Input: given a $N \times N$ filled with $S \times S$ boxes, and an integer $M$ represented in unary.
Question: can the $S \times S$ boxes be packed in the upper-left corner (home area) using at most $M$ column or row shifts?
Open problem: what is the complexity of the Box Shift Puzzle? Is it NP-complete?
Also the following variants (or any combination of them) seem interesting:
- V1. in addition to the initial configuration, a target configuration is given and the problem is to decide if the initial configuration can be transformed into the target configuration using at most $M$ moves;
- V2. one of the side of the grid is fixed (the size of the grid is $N \times k$);
- V3. the columns (resp. rows) can be moved in both up-down directions (resp. left-right);
- V4. the boxes cells could be colored with colors in $[1..c]$
… I’ll spend some time on it, if I find something interesting I’ll update this page.