Tag Archives: NP-completeness

Box Shift Puzzle

Posted on by
Reply

While thinking about simple “puzzles” that seem hard at a first glance, but have not enough rules and structural constraints that make it easy to prove that they are NP-complete, I designed the following game (but perhaps it has already a name … let me know if you know it 🙂 ):

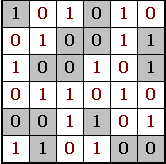
  • a $N \times N$ grid contains $S \times S$ blue boxes in the upper left area, the home area; each box occupies a cell;
  • a column (or row) that contains at least one box is picked at random and it is shifted downward (or rightward). If a box exits from one border it re-enters on the opposite site;
  • the random shift is repeated maxmoves times (e.g. $maxmoves = S^2$);
  • the aim of the game is to repack the boxes in the upper left home area, using at most maxmoves upward column shifts or leftward row shifts.

A simple javascript version of the game can be played here.

Can the blue boxes be packed in the upper-left 4×4 yellow area using at most 16 moves?

The rules are simple, but even in a small game with a 4×4 home area it’s hard to find the correct shift sequence …

Continue reading →

Minimizing the COL4 to COL3 reduction

Posted on by
Reply

I just bought the nice book “Problems with a POINT – Exploring Math and Computer Science” by William Gasarch and Clyde Kruskal. The book explains many nice mathematical and theoretical computer science problems that are “easy-to-understand-but-not-so-easy-to-solve”, and most of them solicit the reader’s curiosity and invite him to futher explore the related topics (plenty of references are given at the end of each chapter).

Chapter 23 explains a sane reduction between COL4 (the problem of deciding whether a graph is 4-colorable) to COL3 (the problem of deciding whether a graph is 3-colorable). Both are well known NP-complete problems. I started reading the chapter, but suddenly stopped and tried to figure out a reduction by myself.

The idea presented in the book is to replace each node of the graph $G$ of the COL4 problem with four nodes, force them to be colorable with colors F and T (the third color R is not allowed), force exactly one of them to be T, and finally adding a gadget that prevents two adjacent quadruples from having two corresponding nodes colored with T.

I came up with a very similar reduction, but the gadgets involved are slightly smaller: indeed a 4 colorable node can be represented “in binary” with two nodes each one colorable with T or F (two bits).

Continue reading →

NPC Pill #5: (P)izza =?= (NP)izza

Posted on by
1

Recently A. Amarilli (a3nm) posted a question on cs.stackexchange.com about the computational complexity of a Test Round problem of the Google France #Hash Code 2015: the “Pizza Regina” problem (March 27th, 2015):

Definition [Pizza Regina problem]

Input: A grid $M$ with some marked squares, a threshold $T\in \mathbb{N}$, a maximal area $A \in\mathbb{N}$

Output: The largest possible total area of a set of disjoint rectangles with integer coordinates in $M$ such that each rectangle includes at least $T$ marked squares and each rectangle has area at most $A$.

The problem can be converted to a decision problem adding a parameter $k \in \mathbb{N}$ and asking:

Question: Does there exist a set of disjoint rectangles satisfying the conditions (each rectangle has integer coordinates in $M$, includes at least $T$ marked squares and has area at most $A$) whose total area is at least $k$ squares?

The problem is clearly in $\mathsf{NP}$, and after struggling a little bit I found that it is $\mathsf{NP}$-hard (so the Pizza Regina problem is $\mathsf{NP}$-complete). This is a sketch of a reduction from MONOTONE CUBIC PLANAR 1-3 SAT:
Continue reading →

NPC Pill #4: Square-Free Subset Product

Posted on by
Reply

While thinking about possible answers to the question “Listing of strongly NP-complete problems” I came up with this simple numeric strongly NP-complete problem:

[SQUARE-FREE SUBSET PRODUCT] Given $3N$ integers, find $N$ of them whose product is square free.

I didn’t find it anywhere, so it can be somewhat “original”.

Continue reading →

NPC Pill #3: Pick 3 or Pick 2 … another NP-complete 3DM variant

Posted on by
Reply

NPC Pills (NP-Complete pills) is a collection of some NP-completeness proofs that I posted on the Q&A sites cstheory.stackexchange.com and cs.stackexchange.com. Up to my knowledge they are original and some of them are not so trivial. At present, most of them are just sketches that contain the NP-hardness reduction idea, but for some of them I wrote (or I’m going to write) a more formal paper. If you are particularly interested in one of them write me an email.

NPC Pill #3: Pick 3 or Pick 2 … another NP-complete 3DM variant

The following variant of the 3-Dimensional Matching problem (3DM) was posted on cstheory.stackexchange.com, a question and answer site for professional researchers in theoretical computer science and related fields:

Definition. 3-DIMENSIONAL MATCHING VARIANT
Input: Set $M \subseteq X \times Y \times Z$ where $X,Y,Z$ are disjoint sets; we call $M_{XY}= \{(x,y)\mid \exists z \text{ s.t. } (x,y,z)\in M \}$ the set of pairs of $X \times Y$ that appear in the triples of $M$, and $M_{XZ}= \{(x,z)\mid \exists y \text{ s.t. } (x,y,z)\in M \}$ the set of pairs of $X \times Z$ that appear in the triples of M.
Question: Does there exist a set $M’ \subseteq M \cup M_{XY} \cup M_{XZ} $ such that every element of $X \cup Y \cup Z$ is included in a triple or a pair of $M’$ exactly once?

Informally we want to build an exact cover of $X \cup Y \cup Z$ using the triples of $M$ or one of the two pairs $(x,y), (x,z)$ that are contained in a triple $(x,y,z) \in M$.

The problem is NP-complete, click the following link to download the technical report with the reduction (we also discuss some other variants of the problem).

Click here to download the technical report

If you have some comments or find some errors, contact me via email.

 

NPC Pill #2: Minimal TSP Tour is coNP-Complete

Posted on by
Reply

NPC Pills (NP-Complete pills) is a collection of some NP-completeness proofs that I posted on the Q&A sites cstheory.stackexchange.com and cs.stackexchange.com. Up to my knowledge they are original and some of them are not so trivial. At present, most of them are just sketches that contain the NP-hardness reduction idea, but for some of them I wrote (or I’m going to write) a more formal paper. If you are particularly interested in one of them write me an email.

NPC Pill #2: Minimal TSP Tour is coNP-Complete

The Traveling Salesman Problem (TSP) is a well–known problem from graph theory: we are given $n$ cities and a nonnegative integer distance $d_{ij}$ between any two cities $i$ and $j$ (assume that the distances are symmetric, i.e. for all $i,j, d_{ij} = d_{ji}$). We are asked to find the shortest tour of the cities, that is a permutation $\pi$ of $[1..n]$ such that
$\sum_{i=1}^n d_{\pi(i),\pi(i+1)}$ (where $\pi(n+1) = \pi(n)$) is as small as possible. Its well-known NP-complete version is the following (TSPDECISION): If a nonnegative integer bound $B$ (the traveling salesman’s “budget”) is  given along with the distances, does there exist a tour of all the cities having total length no more than $B$?

But what about checking that a tour has effectively minimal length? We prove that the problem:

TSPMINDECISION: Given  a set of $n$ cities, the distance between all city pairs and a tour $T$, is T visiting each city exactly once and is T of minimal length?

is coNP-complete. As a secondary result we prove that given a graph $G$ and an Hamiltonian path, it is NP-complete to check if $G$ contains an Hamiltonian cycle as well.

UPADTE 2014-03-21: after publishing the proof on arXiv, it turned out that the same result was proved Papadimitriou and Steiglitz in [1] (see also [2] Section 19.9). Our proof is slightly different and it may be interesting in and of itself, so we decided not to withdraw the paper.

[1] Christos H. Papadimitriou and Kenneth Steiglitz. 1982. Combinatorial Optimization: Algorithms and Complexity. Prentice-Hall, Inc., Upper Saddle River, NJ, USA.
[2] Christos H. Papadimitriou and Kenneth Steiglitz. On the Complexity of Local Search for the Traveling Salesman Problem. SIAM J. Comput., 6(1), 76–83, 1977.

NPC Pill #1: Single Overlap RX3C

Posted on by
1

NPC Pills (NP-Complete pills) is a collection of some NP-completeness proofs that I posted on the Q&A sites cstheory.stackexchange.com and  cs.stackexchange.com. Up to my knowledge they are original and some of them are not so trivial. At present, most of them are just sketches that contain the NP-hardness reduction idea, but for some of them I wrote (or I’m going to write) a more formal paper. If you are particularly interested in one of them write me an email.

NPC Pill #1: SINGLE OVERLAP RX3C

The EXACT COVER BY 3-SETS (X3C) problem is:

Instance: Set $X = \{x_1,x_2,…,x_{3q}\}$ and a collection $C = \{C_1,…,C_m\}$ of 3-element subsets of $X$.
Question: Does $C$ contain an exact cover for $X$, i.e. a subcollection $C’ \subseteq C$ such that every element of $X$ occurs in exactly one member of $C’$?

X3C is NP-complete [1], and as shown in [2] it remains NP-complete even if every element $x_i$ contained in exactly 3 subsets of $C$ (Restricted Exact Cover by 3-Sets – RX3C).

We proved that it remains NP-complete even if every pair of subsets in $C$  share at most one element; i.e. for all $i \neq j,\; | C_i \cap C_j | \leq 1$ and we call this restricted version SINGLE OVERLAP RX3C.

[1] M. R. Garey, David S. Johnson: Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman 1979, ISBN 0-7167-1044-7.
[2] Teofilo F. Gonzalez: Clustering to Minimize the Maximum Intercluster Distance. Theor. Comput. Sci. 38: 293-306 (1985).

 

Weapon-target assignment problem

Posted on by
Reply

The decision version of the Weapon-Target Assignment (WTA) problem is as follows:

There are a number of weapons and a number of targets. The weapons are of type $i = 1, \ldots, m$ . There are $W_{i}$ available weapons of type $i$. Similarly, there are $j = 1, \ldots, n$ targets, each with a value of $V_{j}$ . Any of the weapons can be assigned to any target. Each weapon type has a certain probability of destroying each target, given by $p_{i,j}$ . Does there exist a weapon-target assignment such that:

$$D = \sum_{j=1}^n V_j \prod_{i=1}^m q_{i,j}^{x_{i,j}} \leq k$$

where $k$ is a given integer; $x_{i,j} = 1$ if weapon $i$ is assigned to target $j$, $x_{i,j} =0$ otherwise; $q_{i,j} = 1 – p_{i,j}$ is the survival probability of target $j$ when hit by weapon $i$. No more than $W_i$ weapons of type $i$ can be used, so we must add the following constraint:

$$\sum_{j=1}^n x_{i,j} \leq W_i \quad \mbox{ for } i = 1,\ldots,m$$

WTA problem is NP complete (see L. Chen, C. J. Ren, and S. Deng, “An efficient approximation for weapon-target assignment,” vol. 1, Computing, Communication, Control, and Management. ISES International Colloquium, 2008, pp. 764-767), we give an alternate hardness proof using a reduction from the NP-complete SUBSET PRODUCT problem. Continue reading →

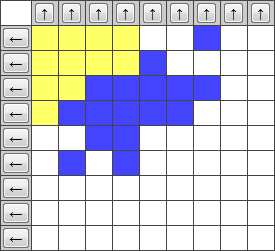
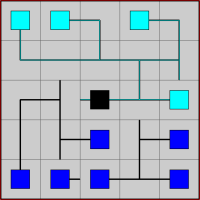
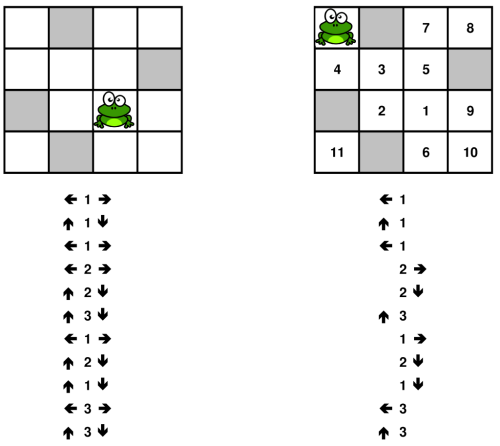The Crazy Frog Puzzle and Permutation Reconstruction from Differences

Posted on by
Reply

The Crazy Frog Puzzle (CFP) is the following: we have a $n \times n$ partially filled board, a crazy frog placed on an empty cell and a sequence of horizontal, vertical, and diagonal jumps; each jump has a fixed length and two possible opposite directions. The crazy frog must follow the sequence of jumps, and at each step it can only choose among the two available directions. Can the frog visit every empty cell of the board exactly once (it cannot jump on a blocked cell and on the same cell two times)?

 Crazy Frog PuzzleFigure 1: an example of the Crazy Frog Puzzle on the left and its solution on the right.

 We prove that the Crazy Frog Puzzle is $\sf{NP}$-complete even if restricted to 1 dimension and even without blocked cells. The 1-D CFP without blocked cells corresponds to the problem of reconstructing a permutation from its differences:

Permutation Reconstruction from Differences problem:
Input: a set of $n-1$ distances $a_1,a_2,…,a_{n-1}$
Question: does exist a permutation $\pi_1,…,\pi_n$ of the integers $[1..n]$ such that $| \pi_{i+1} – \pi_i| = a_i$, $i=1,…,n-1$ ?

For example, given the differences $(2,1,2,1,5,3,1,1)$ a valid permutation of $[1..9]$ is $(5,7,6,8,9,4,1,2,3)$

Update 2013-12-19: a new version of the paper is available.

The Complexity of Crazy Frog Puzzle and Permutation Reconstruction from Differences click here to download a draft of the paper

 

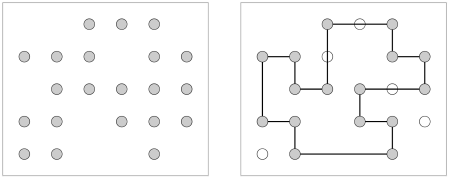Complexity of the Hidden Polygon Puzzle

Posted on by
Reply

The Hidden Polygon Puzzle (for brevity HPP) decision problem  is:

Input: a set $P$ of $m$ integer points on a $n \times n$ square grid and an integer $k \leq m$;

Question: does exist a simple rectilinear polygon with $k$ or more vertices $(v_1,v_2, …, v_t), \; v_i \in P, t \geq k$?

The following figure shows an example of a HPP puzzle.

Hidden Polygon PuzzleFigure 1: Given the 21 points on the right, can we find
a simple rectilinear polygon with at least 16 vertices?
A possible solution is shown on the right.

The problem is a slight variant of the $\sf{NP}$-complete puzzle game Hiroimono; we prove that the Hidden Polygon Puzzle is  $\sf{NP}$-complete, too using a completely different reduction.

click here to download the paper

Hidato is NP-complete

Posted on by
Reply

Hidato (also known as Hidoku) is a logic puzzle game invented by Dr. Gyora Benedek, an Israeli mathematician. The rules are simple: given a grid with $n$ cells some of which are already filled with a number between $1$ and $n$ (the first and the last number are circled), the player must completely fill the board with consecutive numbers that connect horizontally, vertically, or diagonally.

corner

Figure 1: An Hidato game (that fits on a $8 \times 8$ grid) and its solution on the right.

We prove that the corresponding decision problem $\sf{HIDATO}$ : “Given a Hidato game that fits in a $m \times n$ grid, does a valid solution exist?” is $\sf{NP}$-complete.

Continue reading →

Binary Puzzle is NP-complete

Posted on by
Reply

Net puzzleBinary Puzzle (also known as Binary Sudoku) is an addictive puzzle played on a $n \times n$ grid; intially some of the cells contain a zero or a one; the aim of the game is to fill the empty cells according to the following rules:

  • Each cell should contain a zero or a one and no more than two similar numbers next to or below each other are allowed
  • Each row and each column should contain an equal number of zeros and ones
  • Each row is unique and each column is unique

We prove that the decision version of Binary Puzzle is NP-complete.

click here to download the paper

Two bits are enough for a “hard” sum

Posted on by
3

On Jan 17 I asked the following question on cs.stackexchange.com:

What is the complexity of the following variant of the SUBSET-SUM decision problem?

2-BIT SUBSET SUM: Given an integer $m \geq 0$, and a set of nonnegative integers $A = \{x_1, x_2, …, x_n\}$ such that every $x_i$ has at most $k=2$ bits set to $1$ ($x_i = 2^{b_{i_1}}+2^{b_{i_2}},\;\; b_{i_1},b_{i_2}\geq 0$); is there a subset $A’ \subseteq A$ such that the sum of its elements is equal to $m$ ?

Continue reading →

The complexity of the puzzle game Net: rotating wires can drive you crazy

Posted on by
Reply

An amateur proof that the puzzle game Net is NP-complete.

Net puzzleAbstract
The puzzle game Net, also known as FreeNet or NetWalk, is played on a grid filled with terminals and wires; each tile of the grid can be rotated and the aim of the game is to connect all the terminals to the central power unit avoiding closed loops and open-ended wires. We prove that Net is NP-complete.

click here to download the paper