Hidato (also known as Hidoku) is a logic puzzle game invented by Dr. Gyora Benedek, an Israeli mathematician. The rules are simple: given a grid with $n$ cells some of which are already filled with a number between $1$ and $n$ (the first and the last number are circled), the player must completely fill the board with consecutive numbers that connect horizontally, vertically, or diagonally.
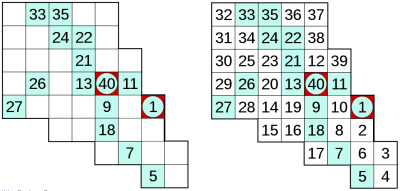
Figure 1: An Hidato game (that fits on a $8 \times 8$ grid) and its solution on the right.
We prove that the corresponding decision problem $\sf{HIDATO}$ : “Given a Hidato game that fits in a $m \times n$ grid, does a valid solution exist?” is $\sf{NP}$-complete.
First we show that the problem is $\sf{NP}$-hard using a polynomial time reduction from the Hamiltonian cycle problem on grid graphs (with holes) which is $\sf{NP}$-complete [1]. Given a grid graph $G = (V,E)$, whose vertices are a subset of the square grid graph $Q = \{ (x,y) : 0 \leq x,y \leq w \}$ (for simplicity we assume that the square has even sides $w=2a$), we can identify the nodes of $G$ with their integer grid coordinates: $V \subseteq \{ (x,y), \; 0 \leq x,y < w \}$ (note that in $Q$ there is always an extra column and an extra row) and without loss of generality we can assume that its upper left corner contains two nodes $s, t$ at coordinates (0,0) and (0,1). If $G$ has an Hamiltonian cycle then the edge $(s,t)$ is part of it (red lines in Figure 2).
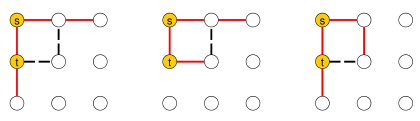
Figure 2: Possible traversals of the two top-left nodes of graph $G$.
- First we expand $G$ adding the missing nodes of the embedding square: $H= \{ (x,y) : (x,y)\in Q \setminus V\} $;
- then we double the coordinates of the points of both $V$ and $H$ and translate them by one: $(x’,y’)=(2x+1,2y+1)$;
- we add a set $K$ of $(w+1) \times (w+1)$ nodes with even coordinates: $K = \{ (2x,2y) : 0 \leq x,y \leq w \}$;
- finally we further expand $K$ adding points $\{ (x,y) : x,y \mbox{ odd} \}$ and $\{ (x,y) : x,y \mbox{ even} \}$ to make $V \cup H \cup K$ a diamond.
The construction steps are shown in Figure 3.
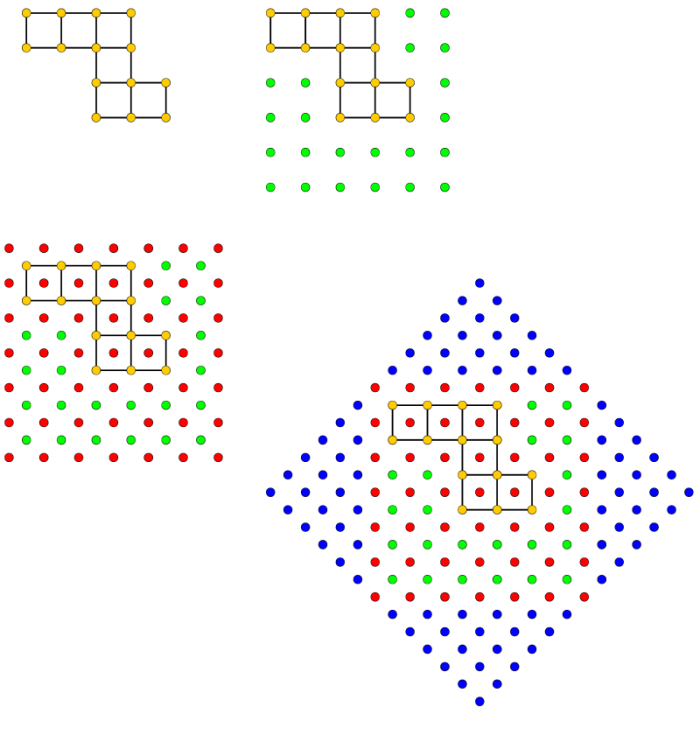
Figure 3: Yellow nodes represent the original graph $G$, green nodes represent the nodes in $H$, red nodes represent the nodes in $K$, blue nodes represent the final expansion to make the whole graph a “diamond” .
Now starting from point $P_1 = (0,0)$ we can build a path $P$ adding $|H|+|K|-1$ edges: we first visit $P_2=(1,-1)$ and $P_3=(2,-2)$ then we join vertically the points $P_i=(x,y)\rightarrow P_{i+1}=(x,y+2)$ in $K$ (downward direction), taking care to inlude points in $H$ when they are present on the left: $(x,y)\rightarrow (x-1,y+1) \rightarrow (x,y+2)$. Once we reach the bottom of the diamond we can leave an unconnected node and continue joining points $(x,y)\rightarrow (x,y-2)$ (upward direction). Once reached the right part of the diamond we can “transfer” to the left using the unconnected nodes at the bottom and connect in a similar manner the leftmost part until we reach point $P_{c} = (0,1), \; c = |H|+|K|$.
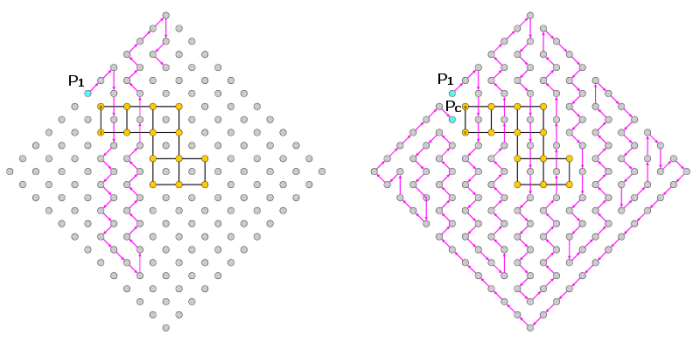
Figure 4: The construction of path $P_1,P_2,…,P_c$.
If we rotate the diamond 90 degrees counterclockwise, we get a $(2w+1) \times (2w+1)$ square grid $Q’$ where each cell corresponds to a node. We can mark the points $P_i$ of the path with numbers $1,2,…,c$, and the node $s$ of the original graph $G$ (at coordinates $(1,1)$) with number $c + |V| = (2w+1) \times (2w+1)$. The other $|V|-1$ nodes are left empty. $Q’$ is a Hidato game and it has a solution if and only if the graph $G$ has an Hamiltonian cycle.
($\Rightarrow$) suppose that $Q’$ has a valid solution; then the first number of the solution is the node $t$ of the original graph and it must be numbered $c+1$ (previous numbers are all fixed); then the next empty cells can be reached only through the diagonals of $Q’$ which correspond to the orthogonal edges of $G$. Each cell is uniquely numbered, and the final cell of the solution is $s$ (numbered with $c+|V|$), so the sequence of cells determines a simple path from $t$ to $s$ in $G$, but the two nodes are connected, so it is also an Hamiltonian cycle.
($\Leftarrow$) suppose that $G$ has an Hamiltonian cycle, then it is enough to follow it from node $t$ to node $s$ and mark the corresponding cells with number $c+1, c+2, …, c + |V|$. By construction the numbers $1,2,…,c$ are valid, and the next numbers (corresponding to the Hamiltonian cycle) are valid, too, because orthogonals moves on $G$ correspond to valid diagonal moves on $Q’$.
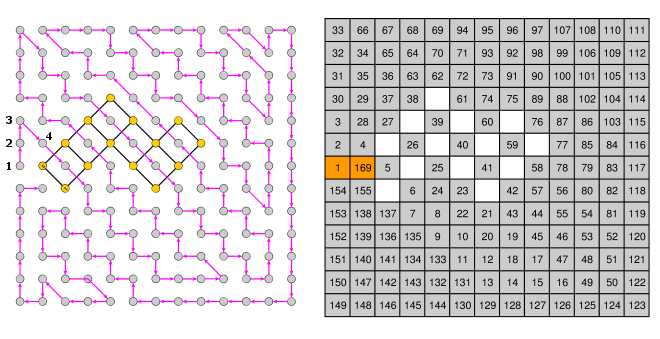
Figure 5: The final Hidato game $Q’$ which has a solution if and only if the starting graph $G$ has an Hamiltonian cycle.
The construction of $Q’$ from $G$ can be done in polynomial time (the sets $H, K$ can be calculated in $O(w^2)$, and the calculation of the initial fixed $c$ numbers takes $O(w^2)$ time, too, so Hidato is $\sf{NP}$-hard.
If we assume that the input of the game is given with an array of $m \times n$ integers containing the initial fixed numbers of the cells (0 if the cell is empty), then it is easy to see that a solution can be verified in polynomial time ($O(m \times n)$).
So if the input is given as an array of integers and we drop the unique solution constraint Hidato is $\sf{NP}$-complete.
$\Box$
A final note: if we add the constraint that the solution must be unique then the problem is US-hard (Unique Polynomial Time), but US contains co-NP, so it is co-NP-hard, too and therefore unlikely to be in NP.
[1] Alon Itai, Christos H. Papadimitriou, Jayme Luiz Szwarcfiter: Hamilton Paths in Grid Graphs. SIAM J. Comput. 11(4): 676-686 (1982)
![]() click here to download the pdf version of this page
click here to download the pdf version of this page
Date: April 2013
Author: Marzio De Biasi
Email: marziodebiasi [at] gmail [dot] com
